A technical side note to my first "A computer from scratch" post and In preparation for the next step, I've examined whether it's possible to build any gate from NANDs. Is it possible? YES! Let's prove it, mathematically.

Theorem

Any truth table can be built by combining NANDs.

Lemma 1

Any truth table can be built with OR, AND and NOT.

Proof

Any truth table is defined by N bits in input (i₁, i₂, …, i_k, …, i_N). A truth table will also have 2^N outputs (out₁, out₂, …, out_l, …, out_2^N).

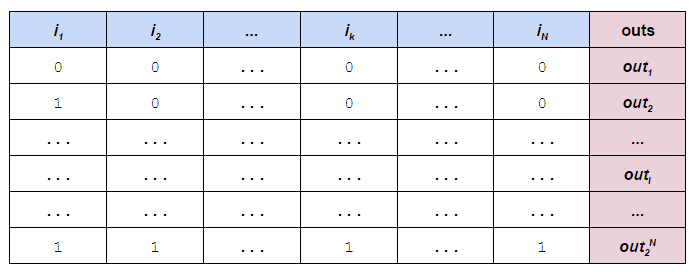
We want to create an expression with only OR, NOT and AND that "represents" each row of inputs, in other words:

• if out_l is 1, then the expression is equal to 1 if and only if all the input match the given inputs
• if out_l is 0, then the expression is equal to 0 independently from the inputs

This allows us to combine all the expression through OR to obtain an expression for the truth table.

In case of out_l = 0 the function is easy to build. It's always the function 0, which can be elided from the whole-expression OR later.
In case of out_l = 1, for each input we will create a sub expression which is valued 1 if the input matches with the given value for the row, and zero otherwise. ANDing all these together will give us an expression as required (its value will be 0 if any input doesn't match, otherwise 1).

How do we create these subexpressions? If the expected input value is 0 then NOT i, if the expected input value is 1 then i.

Example

An example will make everything clear. Let's create an expression to represent the following truth table:

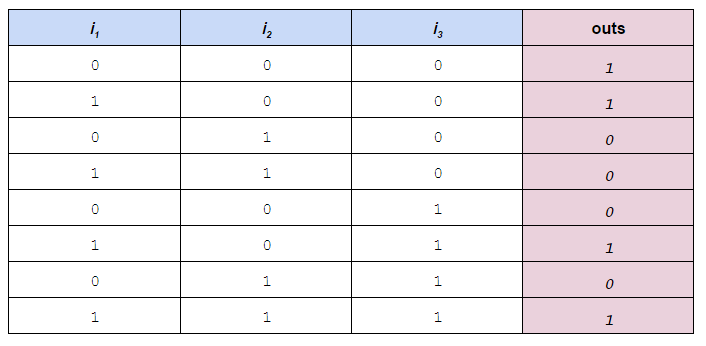
1. Let's ignore all lines with value 0.

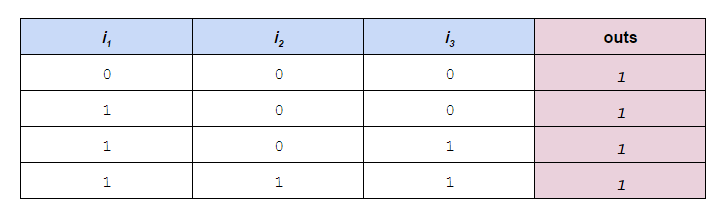
1. Let's write in i_k in place of all the 1s and NOT i_k in place of all the 0s.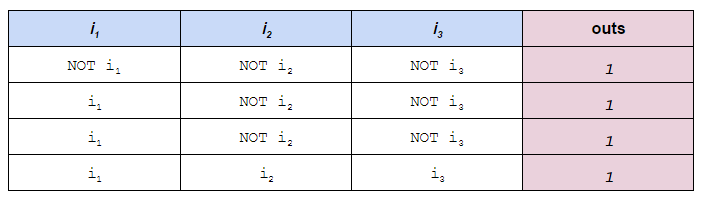

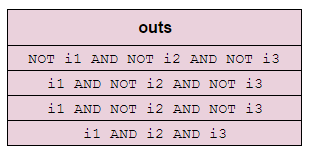
1. Let's AND all columns for each row and put the output in the out cell.

1. Finally, ORing together all the rows will give us our final expression.

(NOT i1 AND NOT i2 AND NOT i3) OR (i1 AND NOT i2 AND NOT i3) OR (i1 AND NOT i2 AND NOT i3) OR (i1 AND i2 AND i3)

Lemma 2

AND, OR and NOT can be expressed in terms of NANDs

Proof

It's easy to see that

NOT a = a NAND a

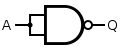
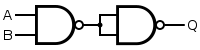
By definition:

a AND b = NOT (a NAND b)

And therefore

a AND b = (a NAND b) NAND (a NAND b)

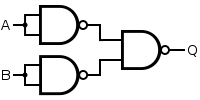
Finally it's easy to verify that

a OR b = (NOT a) NAND (NOT b)

And therefore

a OR b = (a NAND a) NAND (b NAND b)

Proof (of the theorem)

Every truth table can be expressed in terms on NAND gates by construction:

1. We can build an expression with only AND, OR, NOT using lemma 1
2. We can substitute the three expressions for AND, OR and NOT in terms of NAND to get a ginormous, but valid, expression.

References

• NAND logic, Wikipedia
• NAND & NOR Gate as Universal Gate, electrical4u.com

(discuss on HN)